Skip to contents

Jackknife-after-Bootstrap for Networks

Source: vignettes/jab-networks.Rmd
jab-networks.Rmd

In this vignette, we discuss the Jackknife-after-Bootstrap (JaB) algorithm for influential nodes in networks. The JaB algorithm for regression data was proposed by Martin and Roberts (2010) and further studied in Beyaztas and Alin (2013). Here we expand this methodology to network data.

JaB for regression uses outlier, leverage, and influence statistics to quantify influence (see vignette("jab-regression")). In network data, centrality statistics are used to quantify influence. Each centrality statistic measures influence as control over information moving throughout the network.

Generally, larger networks have more complex data structures which are notoriously difficult to exactly quantify. One approach is to identify central nodes whose positions data allow them to influence the movement of objects or information throughout the network. But what does it mean for a node to be central or influential? There is no clear consensus on these definitions and thus dozens of centrality statistics have been proposed to quantify influence Rodrigues (2019).

Nodes with large centrality statistics are influential because of their critical position in the network (Valente et al. 2008). But how large does a centrality statistic need to be in order for the node to be considered influential? While these statistics are very helpful in quantifying each node’s influence, they do not provide a clear answer to this question. It is also not clear if the definition of “large enough to be influential” is the same across all measures of centrality. In this vignette we introduce the Jackknife-after-Bootstrap algorithm for network data that utilizes centrality statistics to answer the question “Which nodes in the network are influential?” It is important to bear in mind that the answer to this question cannot be divorced from the definition of influential. And since there are many proposed definitions, our algorithm is designed to adapt to any centrality statistic.

Centrality Statistics

We begin by introducing a few centrality statistics and defining the types of influence they measure. The igraph package has many useful functions. A network \(G = (V, E)\) consists of two sets, the set of nodes (also called vertices), \(V\), and the set of edges, \(E\). The node set, \(V = \{v_i: i = 1, ..., n\}\), consists of all \(n\) nodes in the network which, without loss of generality, are labeled 1, 2, …, \(n\). The edge set \(E = \{(i,j) : e_{i,j} = 1, i,j = 1,...,n\}\) consists of all edges where \(e_{i,j}=1\) if there exists a connection between nodes \(v_i\) and \(v_j\), and is 0 otherwise. It is often mathematically convenient to arrange the edges in a matrix. Let \(\boldsymbol{A}\) be the of graph \(G\), where \(A_{i,j} = e_{i,j}\) is the \((i,j)^{\text{th}}\) entry of \(\boldsymbol{A}\).

Throughout this section, we will use the karate network as an example. This network represents the members of a university karate club that broke into two factors, one led by John A (circles), and the other by Mr. Hi (squares). The nodes are members of the karate club and and edge is present between two nodes if the two respective actors participated in common activities together.

data("karate")
l <- layout_nicely(karate)
V(karate)$x <- l[,1]
V(karate)$y <- l[,2]

net <- intergraph::asNetwork(karate)

net %v% "shape" <- ifelse(V(karate)$Faction == 1, "circle", "triangle")
delete.vertex.attribute(net, "color")

ggnet2(net,
       label = TRUE, 
       node.shape = "shape",
       mode = c("x", "y"),
       node.label = "label") +
  scale_shape(name = "Faction", labels = c("Mr. Hi", "John A."))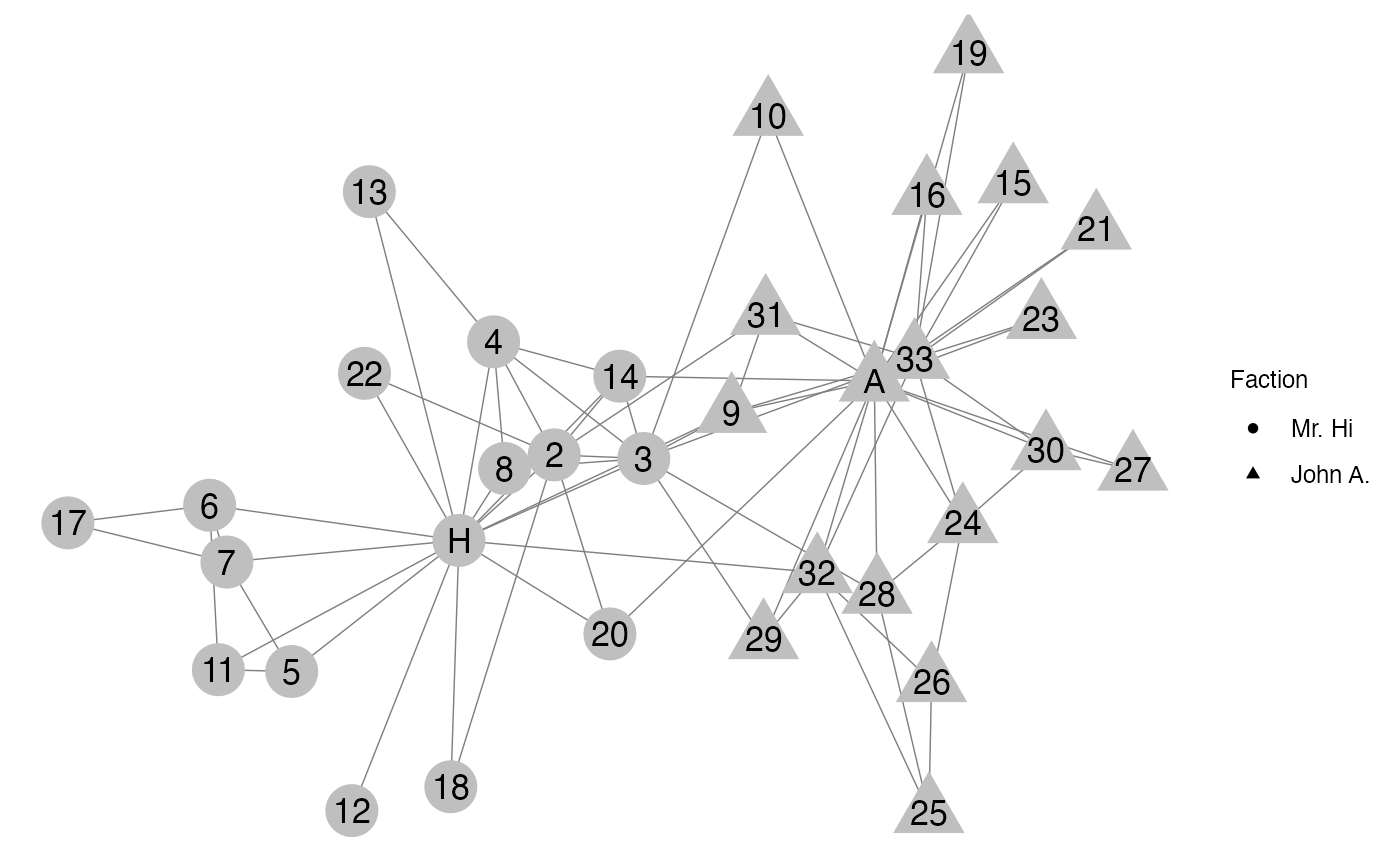

Degree Centrality

One way to measure influence is the number of connections an actor has. If an actor has many connections we consider them influential due to their “popularity” among the other actors, whereas if an actor as relatively few connections we consider them “unpopular”. Degree centrality measures this type of influence. The , \(d_i\), of a node is the number of edges connected to it and is defined through multiple statistics,
\[\begin{equation} \gamma_i^{\text{deg}} = \sum_{j} e_{i,j} = \sum_{j} A_{i,j} = \sum_{i} A_{i,j}. \end{equation}\]

Popular actors will have a large degree as they are connected to many other actors, and unpopular actors will have a small degree as they are connected to only a few actors.

The maximum degree is \(n-1\) and occurs when a node is connected to all other nodes. The minimum degree is \(0\) and occurs when a node is not connected to any other node (i.e. it is isolated). For this reason, degree is often normalized by the constant \(n-1\). \[\begin{equation} \gamma_i^{\text{deg}} = \frac{1}{n-1}\sum_{j} e_{i,j} = \frac{1}{n-1}\sum_{j} A_{i,j} = \frac{1}{n-1}\sum_{i} A_{i,j}. \end{equation}\]

Let’s look at the degree of the karate network. In the plot below light blue nodes have a low degree and dark blue nodes have a high degree. Mr. Hi, John A., and Node 33 have the highest degree values and thus are the most “popular”.

deg <- igraph::degree(karate)
net %v% "deg.cols" <- colour_values(deg, palette = "blues")
ggnet2(net,
       label = TRUE, 
       node.shape = "shape",
       mode = c("x", "y"),
       node.label = "label",
       node.color = "deg.cols") +
  scale_shape(name = "Faction", labels = c("Mr. Hi", "John A."))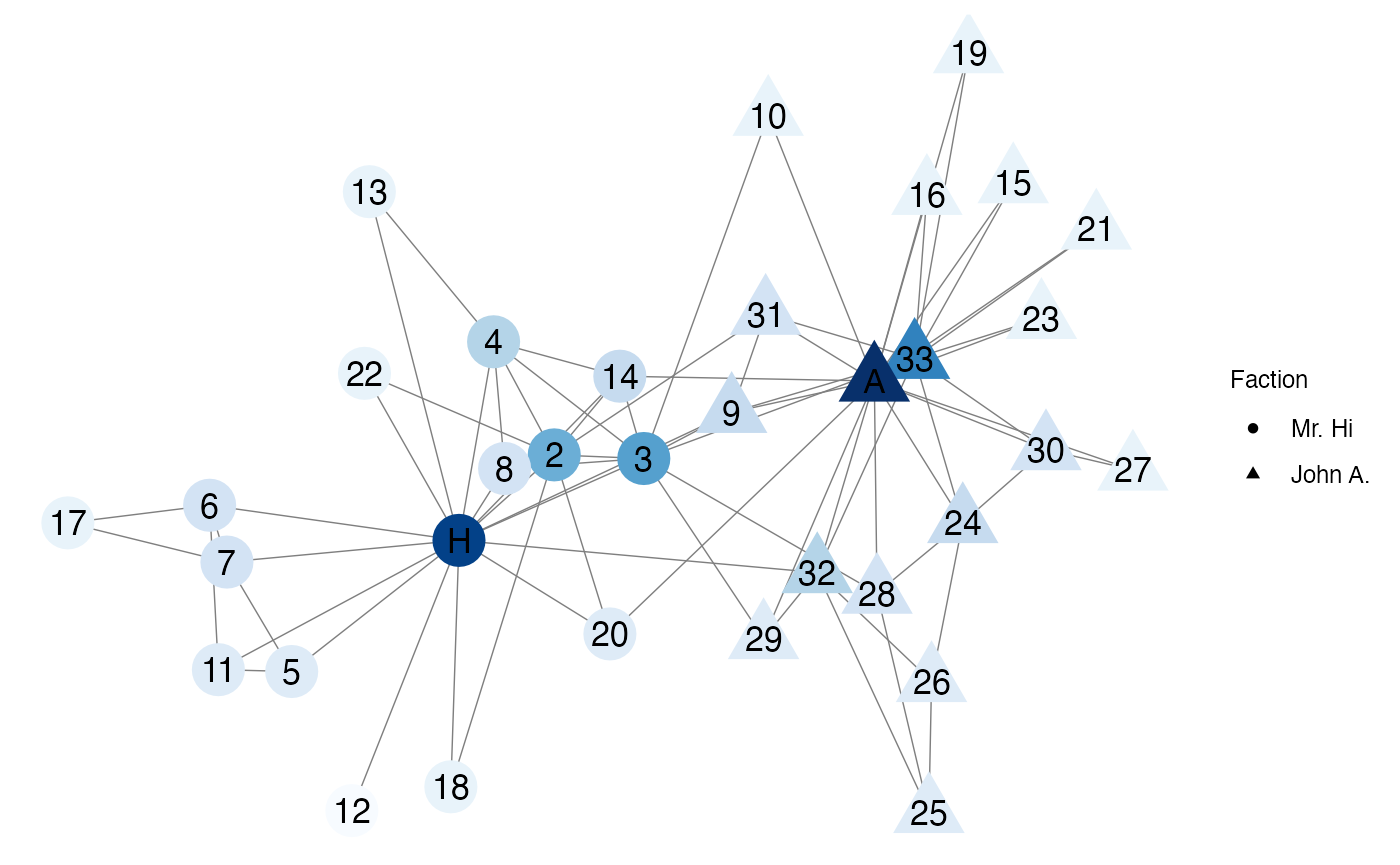

Eigenvector centrality

Degree centrality measures influence as the number of connections a node has. However, it may be the case that not all nodes are equally as important to be connected to. For example, when measuring a node’s popularity, in addition to the number of connections a node has, we may also want to consider how popular those nodes are (Lü et al. 2016). This relational structure is captured by eigenvector centrality (Bonacich 1972). Nodes with high eigenvector centrality are influential because they are closely connected to other nodes that are also influential. Eigenvector centrality is calculated as \[\begin{equation}\label{eqn:eigen} \gamma_i^{\text{ev}} = \frac{1}{\lambda} \sum_{j=1}^n A_{i,j}\gamma_j^{\text{ev}}. \end{equation}\]

In the karate network, Node 3 has a large eigenvector centrality because it is connected to Mr. Hi and Actor 33, both of which also have large eigenvector centralities.

ev <- igraph::eigen_centrality(karate)$vector
net %v% "ev.cols" <- colour_values(ev, palette = "blues")
ggnet2(net,
       label = TRUE, 
       node.shape = "shape",
       mode = c("x", "y"),
       node.label = "label",
       node.color = "ev.cols") +
  scale_shape(name = "Faction", labels = c("Mr. Hi", "John A."))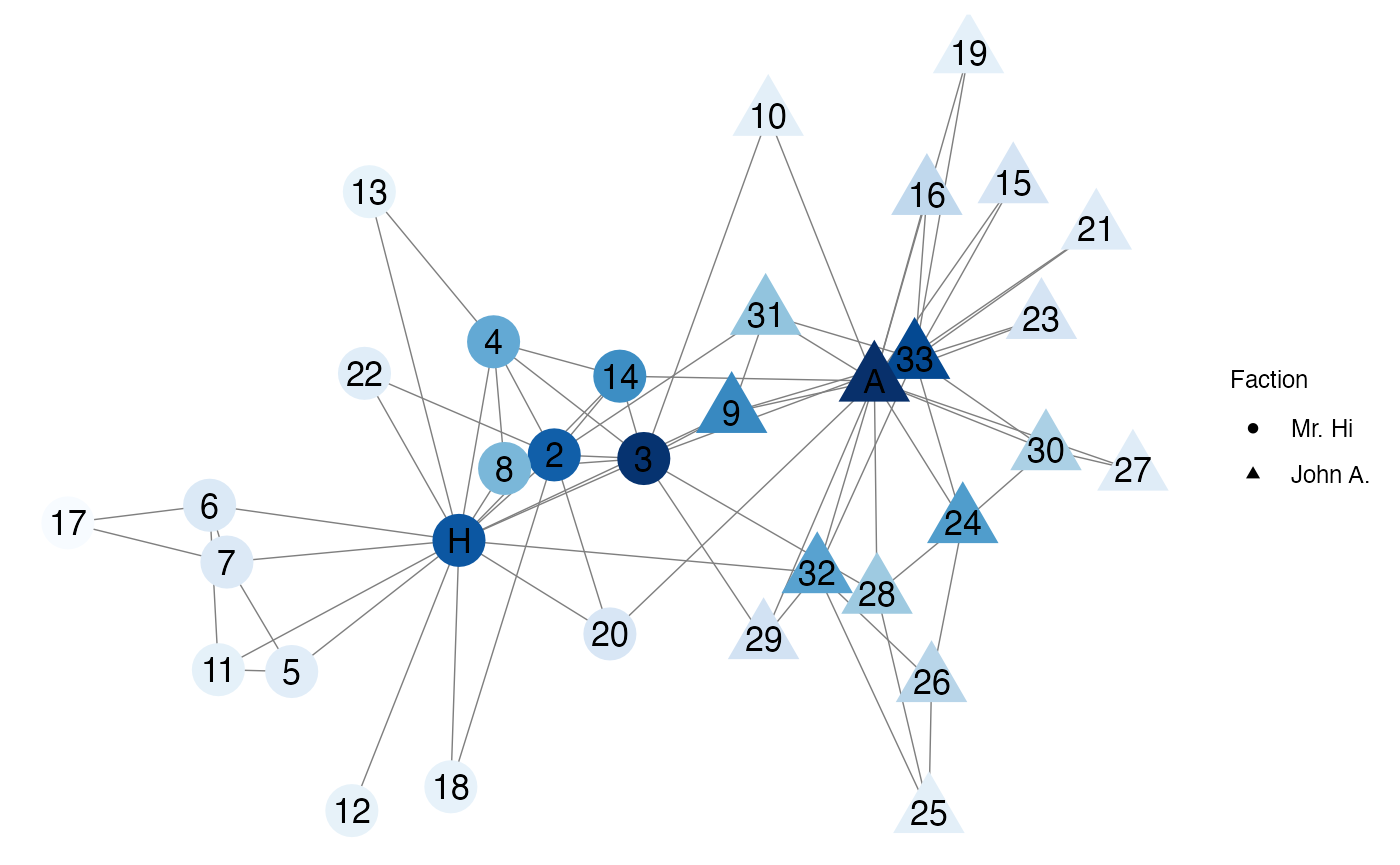 


# Connections of Node 3
igraph::neighborhood(karate, order = 1, nodes = 3)
#> [[1]]
#> + 11/34 vertices, named, from 4b458a1:
#>  [1] Actor 3  Mr Hi    Actor 2  Actor 4  Actor 8  Actor 9  Actor 10 Actor 14
#>  [9] Actor 28 Actor 29 Actor 33

Closeness Centrality

Closeness centrality is a distance-based metric that captures how central a node is to the network (bavelas-1950?). The closeness of node \(i\) is the reciprocal of the average distance along the shortest paths from node \(i\) to the other \(n-1\) nodes in the network. Close'' nodes are those with large closeness values as they have short average distance to all other nodes in the network and are influential due to their ability to receive and disseminate information quickly and directly to every other node in the network.Far’’ nodes are those with small closeness values because they have a long average distance to all other nodes.

Mr. Hi, John A., and Node 33 have large closeness centralities because they have large degree values. Nodes with large degree values tend to have large closeness centralities due to their highly connected positions in the network. Additionally, Node 20 has a high closeness centrality because it is connected to two highly connected nodes (Mr. Hi and John A.).

close <- igraph::closeness(karate)
net %v% "close.cols" <- colour_values(close, palette = "blues")
ggnet2(net,
       label = TRUE, 
       node.shape = "shape",
       mode = c("x", "y"),
       node.label = "label",
       node.color = "close.cols") +
  scale_shape(name = "Faction", labels = c("Mr. Hi", "John A."))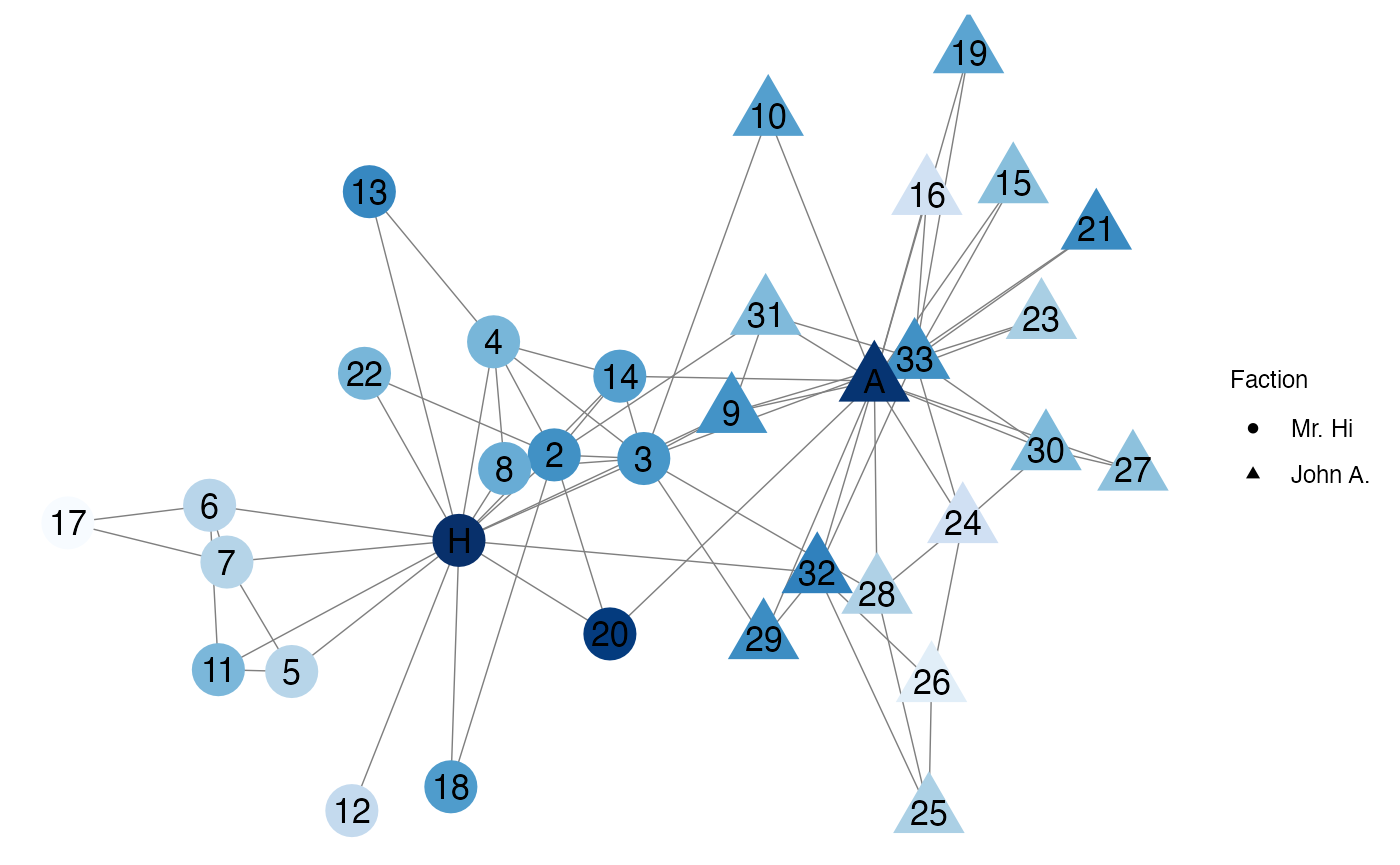 


igraph::neighborhood(karate, order = 1, nodes = 20)
#> [[1]]
#> + 4/34 vertices, named, from 4b458a1:
#> [1] Actor 20 Mr Hi    Actor 2  John A

Jackknife-after-Bootstrap

As described in vignette("jab-regression"), the JaB algorithm in regression identifies influential points. This algorithm has a direct analogy to network data. Using centrality statistics, we can detect influential nodes in networks as follows:

For each node in the network \(G=(V,E)\), we test the hypotheses \(H_0\): node \(i\) is not influential to the network, versus \(H_1\): node \(i\) is influential to the network.

Specify a centrality statistic, \(\gamma\), that quantifies the type of influence we want to measure. Define \(q\in [0, 1]\) to be the upper quantile cut off value and \(B\) to be the number of bootstrap samples.

The JaB algorithm has three steps:

Step 1 (centrality step): For all \(v_i \in V\), calculate \(\gamma_i\).

Step 2 (bootstrapping step): Generate bootstrap samples \(G^{*b}=(V^{*b}, E^{*b})\) for \(b=1,...,B\). For each bootstrap sample, calculate \(\{\gamma_j^{*b} : j=1,...,n\}\).

Step 3 (jackknife-after step): For \(i=1,...,n\);

  1. Calculate \(S_i^{*b} = \boldsymbol{1}(v_i \in V^{*b})\) for \(b=1,...,B\) and construct \(\mathcal{B}_{-i} = {G^{*b}: S_i^{*b} = 0)\) which is the set of all bootstrap sample networks that contain node \(i\).

  2. Let \(\Gamma\_{-i} = \{\gamma_j^{*b} : G^{*b} \in \mathcal{B}_{-i}, j=1,...,n\}\) be the set of all centrality statistics calculated from all bootstrap sample networks that contain node \(i\).

  3. Calculate the cutoff value, \(q_{-i}\), the \(q^{\text{th}}\) quantile of \(\Gamma_{-i}\).

  4. If \(\gamma_i > q_{-i}\), reject Hypothesis the null hypothesis and conclude data node \(i\) is influential.

Additionally, we use the bootstrap samples generated in Step 2 of the JaB algorithm to construct bootstrap standard errors and confidence intervals. Let \(\mathcal{B}_i = \{G^{*b} : S_i^{*b} = 1\}\) be the set of all bootstrap networks that include \(v_i\) and \(\Gamma_i = \{\gamma_j : v_j^{*b} = v_i , v_j^{*b} \in V^{*b}\}\) be the set of centrality statistics corresponding to the nodes that are sampled to be \(v_i\). Then the bootstrap standard error of \(\gamma_i\) is \[\sigma_i^* = \sqrt{(|\Gamma_i |-1)^{-1} \sum_{\gamma_j \in \Gamma_i} (\gamma_j - \Bar{\gamma}_i)^2}\] where \(\Bar{\gamma}_i = |\Gamma_i|^{-1}\sum_{\gamma_j \in \Gamma_i} \gamma_j\). Using \(\sigma_i^{ *}\), bootstrap confidence intervals are constructed in the traditional way. For example, a 95% bootstrap confidence interval for \(\gamma_i\) is \((\gamma_i - 1.96\sigma_i^{ *} , \gamma_i + 1.96\sigma_i^{ *})\). For many centrality statistics \(\gamma_i\) must be a non-negative value. If it is the case that \(\gamma_i\) must be non-negative and \(\gamma_i - 1.96\sigma_i^{ *}<0\), we set the 95% bootstrap confidence interval to be \((0, \gamma_i + 1.96\sigma_i^{ *})\). By construction \(\mathcal{B}_i \cap \mathcal{B}_{-i} = \emptyset\). The bootstrap samples in \(\mathcal{B}_i\) are used for the bootstrap standard errors and the bootstrap samples in \(\mathcal{B}_{-i}\) are used for the hypothesis test of node \(v_i\)’s influence.

The choice of \(q\)

In JaB for network data, \(q\) is generally only an upper quantile cutoff (opposed to upper and lower as in the case of regression) because centrality statistics are generally only positive; nodes with large centrality statistics are influential and nodes with statistics close to zero are not influential. Thus when detecting influential nodes, we only need to consider the upper tail of the distribution

Notes on Network Bootstrap

Examples

Karate Network 

result <- karate.result <- jab_network(
  network = karate,
  central.func.name = "degree",
  central.package.name = "igraph",
  central.func.args = list(normalized = TRUE),
  bootstrap.func.name = "bootstrap_snowboot" ,
  bootstrap.package.name = "JaB" ,
  bootstrap.func.args = list( num.seed = 1, num.wave = 2 ),
  B = 1000,
  quant = 0.90,
  nodes = NULL,
  return.boot.samples = FALSE)

kable(karate.result) %>% 
  kable_styling()
Node_Number Node_Name Orig_Stat Boot_mean Boot_sd Boot_skew Upper_Quantile Influential Rank Can_Jackknife Num_Boot_Samps
1 Mr Hi 0.4848485 0.1391861 0.1733375 1480.7380 0.2631579 TRUE 1 TRUE 244
34 John A 0.5151515 0.1406782 0.1737237 1473.3565 0.3750000 TRUE 2 TRUE 275
33 Actor 33 0.3636364 0.1410643 0.1739514 1514.4534 0.3750000 FALSE 3 TRUE 247
26 Actor 26 0.0909091 0.1515643 0.1645773 535.6559 0.3333333 FALSE 4 TRUE 687
24 Actor 24 0.1515152 0.1389793 0.1762904 1308.1310 0.4000000 FALSE 5 TRUE 368
6 Actor 6 0.1212121 0.1347489 0.1768465 1097.7574 0.3750000 FALSE 6 TRUE 486
7 Actor 7 0.1212121 0.1347489 0.1768465 1097.7574 0.3750000 FALSE 6 TRUE 486
28 Actor 28 0.1212121 0.1410643 0.1739514 1514.4534 0.3750000 FALSE 6 TRUE 247
17 Actor 17 0.0606061 0.1621258 0.2024164 279.4263 0.3333333 FALSE 9 TRUE 824
30 Actor 30 0.1212121 0.1365459 0.1754419 1315.4058 0.4000000 FALSE 10 TRUE 395
31 Actor 31 0.1212121 0.1375821 0.1746079 1628.9705 0.4000000 FALSE 10 TRUE 253
5 Actor 5 0.0909091 0.1347489 0.1768465 1097.7574 0.3750000 FALSE 12 TRUE 486
11 Actor 11 0.0909091 0.1347489 0.1768465 1097.7574 0.3750000 FALSE 12 TRUE 486
25 Actor 25 0.0909091 0.1462448 0.1560607 538.8548 0.3750000 FALSE 12 TRUE 688
29 Actor 29 0.0909091 0.1410643 0.1739514 1514.4534 0.3750000 FALSE 12 TRUE 247
2 Actor 2 0.2727273 0.1310694 0.1668775 1538.3688 0.6000000 FALSE 16 TRUE 326
10 Actor 10 0.0606061 0.1365664 0.1719945 1535.7280 0.4000000 FALSE 17 TRUE 302
15 Actor 15 0.0606061 0.1334745 0.1739711 1331.7088 0.4000000 FALSE 17 TRUE 423
16 Actor 16 0.0606061 0.1334745 0.1739711 1331.7088 0.4000000 FALSE 17 TRUE 423
19 Actor 19 0.0606061 0.1334745 0.1739711 1331.7088 0.4000000 FALSE 17 TRUE 423
21 Actor 21 0.0606061 0.1334745 0.1739711 1331.7088 0.4000000 FALSE 17 TRUE 423
23 Actor 23 0.0606061 0.1334745 0.1739711 1331.7088 0.4000000 FALSE 17 TRUE 423
27 Actor 27 0.0606061 0.1344875 0.1768988 1246.0929 0.4000000 FALSE 17 TRUE 451
13 Actor 13 0.0606061 0.1300127 0.1709925 1135.8166 0.4166667 FALSE 24 TRUE 513
18 Actor 18 0.0606061 0.1302440 0.1701291 1207.7662 0.4166667 FALSE 24 TRUE 479
22 Actor 22 0.0606061 0.1302440 0.1701291 1207.7662 0.4166667 FALSE 24 TRUE 479
3 Actor 3 0.3030303 0.1399091 0.1795191 1914.9343 0.6666667 FALSE 27 TRUE 88
12 Actor 12 0.0303030 0.1300127 0.1709925 1135.8166 0.4166667 FALSE 28 TRUE 513
4 Actor 4 0.1818182 0.1310694 0.1668775 1538.3688 0.6000000 FALSE 29 TRUE 326
8 Actor 8 0.1212121 0.1286171 0.1672100 1488.9024 0.5555556 FALSE 30 TRUE 357
9 Actor 9 0.1515152 0.1379871 0.1801376 2002.8578 0.6666667 FALSE 31 TRUE 82
14 Actor 14 0.1515152 0.1379871 0.1801376 2002.8578 0.6666667 FALSE 31 TRUE 82
20 Actor 20 0.0909091 0.1379871 0.1801376 2002.8578 0.6666667 FALSE 33 TRUE 82
32 Actor 32 0.1818182 0.1416195 0.1814396 1982.8849 0.8000000 FALSE 34 TRUE 27

References

Beyaztas, U., and A. Alin. 2013. “Jackknife-After-Bootstrap Method for Detection of Influential Observations in Linear Regression Models.” Communications in Statistics-Simulation and Computation 42 (6): 1256–67.
Boldi, P., and S. Vigna. 2014. “Axioms for Centrality.” Internet Mathematics 10 (3-4): 222–62.
Bonacich, P. 1972. “Factoring and Weighting Approaches to Status Scores and Clique Identification.” Journal of Mathematical Sociology 2 (1): 113–20.
Lü, L., D. Chen, X. L. Ren, Q. M. Zhang, Y. C. Zhang, and T. Zhou. 2016. “Vital Nodes Identification in Complex Networks.” Physics Reports 650: 1–63.
Martin, M. A., and S. Roberts. 2010. “Jackknife-After-Bootstrap Regression Influence Diagnostics.” Journal of Nonparametric Statistics 22 (2): 257–69. https://doi.org/10.1080/10485250903287906.
Rodrigues, F. A. 2019. “Network Centrality: An Introduction.” In A Mathematical Modeling Approach from Nonlinear Dynamics to Complex Systems, 177–96. Springer.
Valente, T. W., K. Coronges, C. Lakon, and E. Costenbader. 2008. “How Correlated Are Network Centrality Measures?” Connections (Toronto, Ont.) 28 (1): 16.